摘 要:本文通过精心收集整理的案例,演示了微分方程模型的建立过程,以及微分方程建立起来之后,如何利用Matlab软件通过拟合相关数据获得未知参数的具体数值。最后通过残差的向量2范数和计算树高与实际树高的对比图验证了本方法的有效性。
关键词:微分方程建模;Matlab;lsqcurvefit
中图分类号:G652;TP319 文献标识码:A 文章编号:2096-4706(2018)09-0140-02
Abstract:By elaborately collecting and arranging cases,this paper demonstrates the process of establishing the differential equation model,and how to use Matlab software to fit the relevant data after the differential equation is established,and to obtain the specific value of the unknown parameters. Finally,the validity of the method is verified by comparing the vector 2 norm of residuals and comparing the height of tree height with actual tree height.
Keywords:differential equation modeling;Matlab;lsqcurvefit
0 引 言
微分方程建模是数学建模这门课程的一个重要课题,它在化学工程、自动控制、力学及动力学问题建模、传染病传播控制等领域有着重要应用。微分方程建模也是全国大学生数学建模比赛重要的考点之一,2006年高教社杯全国大学生数学建模比赛B题《艾滋病疗法的评价及疗效的预测》、2007年高教社杯全国大学生数学建模比赛A题《中国人口增长预测》等赛题里都渗透着微分方程建模的思想方法。熟练地学会用Matlab数学软件解决微分方程建模问题对于提高学生数学素养,增强同学动手能力有着很大的帮助,下面是精心整理的微分方程建模案例。
1 案例问题
油松为中国东北某林区的重要经济树种。通过历年经验积累,得到以下树龄和平均树高的资料,如表1所示,试问能否根据此表得出油松每年树高的函数关系式?
2 案例解析
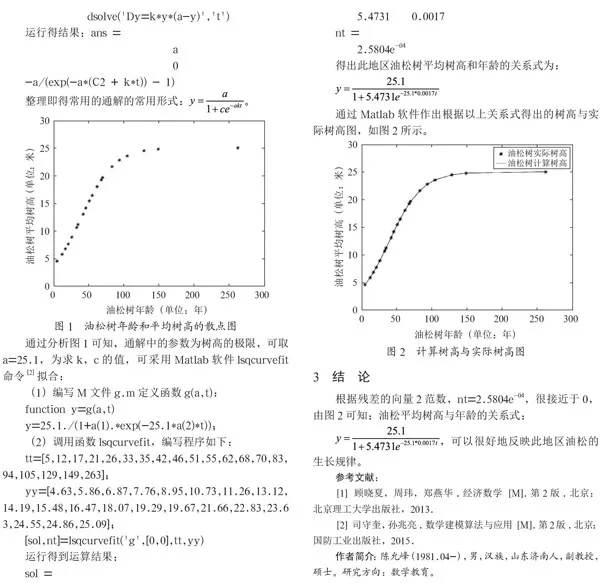
解:我们可以通过Matlab软件画出各年龄油松树高数据的散点图,如图1所示。
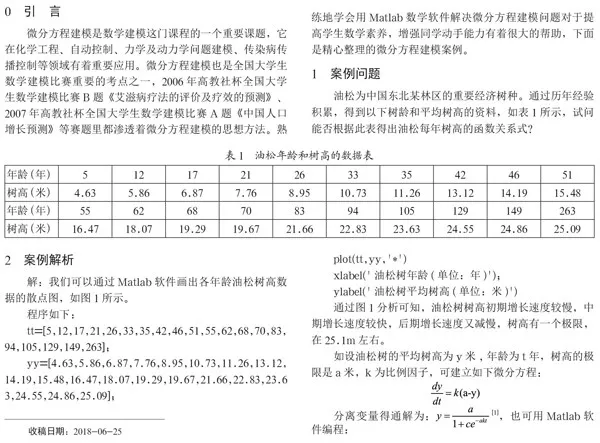
通过图1分析可知,油松树树高初期增长速度较慢,中期增长速度较快,后期增长速度又减慢,树高有一个极限,在25.1m左右。
参考文献:
[1] 顾晓夏,周玮,郑燕华.经济数学 [M].第2版.北京:北京理工大学出版社,2013.
[2] 司守奎,孙兆亮.数学建模算法与应用 [M].第2版.北京:国防工业出版社,2015.
作者简介:陈允峰(1981.04-),男,汉族,山东济南人,副教授,硕士。研究方向:数学教育。




